(本小题满分10分)已知函数 ,
, 在
在 处取得极小值
处取得极小值 。求a+b的值
。求a+b的值
选修4—5:不等式选讲
已知函数f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m-f(-n)成立,求实数m的取值范围.
选修4—4:坐标系与参数方程
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线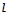 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角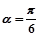 .
.
(1)写出直线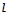 的参数方程;
的参数方程;
(2)设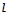 与圆
与圆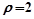 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.
选修4—1:几何证明选讲
D、E分别为△ABC的边AB、AC上的点,且不与△ABC的顶点重合。已知AE的长为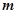 ,AC的长为
,AC的长为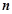 ,AD、AB的长是关于
,AD、AB的长是关于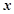 的方程
的方程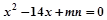 的两个根。
的两个根。
(1)证明:C、B、D、E四点共圆;
(2)若∠A=90°,且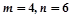 ,求C、B、D、E所在圆的半径。
,求C、B、D、E所在圆的半径。
已知函数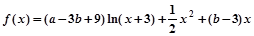 .
.
(1)当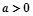 且
且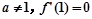 ,时,试用含
,时,试用含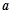 的式子表示
的式子表示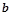 ,并讨论
,并讨论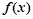 的单调区间;
的单调区间;
(2)若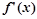 有零点,
有零点,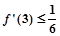 ,且对函数定义域内一切满足|x|≥2的实数x有
,且对函数定义域内一切满足|x|≥2的实数x有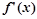 ≥0.
≥0.
①求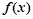 的表达式;
的表达式;
②当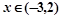 时,求函数
时,求函数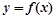 的图象与函数
的图象与函数 的图象的交点坐标.
的图象的交点坐标.