某高校共有学生 人,其中男生
人,其中男生 人,女生
人,女生 人.为调查该校学生
人.为调查该校学生
每周平均体育运动时间的情况,采用分层抽样的方法,收集 位学生每周平均体育运动时间的样本数据(单位:小时).
位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这 个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:
个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为: ,
, ,
, ,
, ,
,
 .估计该校学生每周平均体育运动时间超过
.估计该校学生每周平均体育运动时间超过 小时的概率;
小时的概率;

(3)在样本数据中,有 位女生的每周平均体育运动时间超过
位女生的每周平均体育运动时间超过 小时,请完成每周平均体育运动时间与性别列联表,并判断是否有
小时,请完成每周平均体育运动时间与性别列联表,并判断是否有 %的把握认为“该校学生的每周平均体育运动时间与性别有关”.
%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
已知函数f(x)=-x3+ax2+1(a∈R).
(1)若函数y=f(x)在区间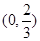 上递增,在区间
上递增,在区间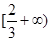 上递减,求a的值;
上递减,求a的值;
(2)当x∈[0,1]时,设函数y=f(x)图象上任意一点处的切线的倾斜角为θ,若给定常数a∈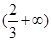 ,求
,求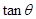 的取值范围;
的取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数g(x)=x4-5x3+(2-m)x2+1(m∈R)的图象与函数y=f(x)的图象恰有三个交点.若存在,求实数m的取值范围;若不存在,试说明理由.
在平面直角坐标系 中,点P到两点(0,-
中,点P到两点(0,-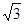 )、(0,
)、(0,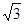 )的距离之和等于4.设点P的轨迹为C.
)的距离之和等于4.设点P的轨迹为C.
(1)写出C的方程;
(2)设直线y=kx+1与C交于A、B两点.k为何值时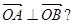 此时|
此时|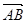 |的值是多少?
|的值是多少?
如图,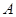 是以
是以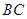 为直径的⊙O上一点,
为直径的⊙O上一点, 于点
于点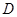 ,过点
,过点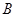 作⊙O的切线,与
作⊙O的切线,与 的延长线相交于点
的延长线相交于点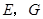 是
是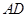 的中点,连结
的中点,连结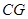 并延长与
并延长与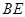 相交于点
相交于点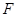 ,延长
,延长 与
与 的延长线相交于点
的延长线相交于点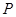 .
.
(1)求证: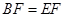 ;
;
(2) 若 , 求
, 求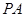 的长.
的长.
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是 .得到了如下列联表:
.得到了如下列联表:
| 男性 |
女性 |
合计 |
|
| 反感 |
10 |
||
| 不反感 |
8 |
||
| 合计 |
30 |
| 男性 |
女性 |
合计 |
|
| 反感 |
10 |
||
| 不反感 |
8 |
||
| 合计 |
30 |
(1)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析是否有百分之九十五以上的把握认为反感“中国式过马路 ”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.附表
| P(K2≥k) |
0.050 |
0.010 |
0.001 |
| k |
3.841 |
6.635 |
10.828 |
如图,⊙ 的直径
的直径 的延长线与弦
的延长线与弦 的延长线相交于点
的延长线相交于点 ,
, 为⊙O上一点,弧AE等于弧AC,
为⊙O上一点,弧AE等于弧AC, 交
交 于点
于点 ,且
,且 ,求
,求 的长度.
的长度.