已知直线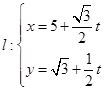 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为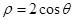 .
.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为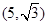 ,直线
,直线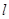 与曲线C的交点为A、B,求
与曲线C的交点为A、B,求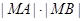 的值.
的值.
(本小题满分14分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且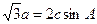 ,
,
(Ⅰ)确定角C的大小
(Ⅱ)若c=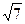 ,且△ABC的面积为
,且△ABC的面积为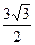
 ,求a+b的值。
,求a+b的值。
(本小题满分12分)
设二次函数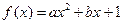 ,若
,若 >0的解集为
>0的解集为 ,函数
,函数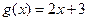 ,
,
(1)求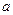 与b的值 ; (2)解不等式
与b的值 ; (2)解不等式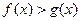
(本小题满分12分)
设等差数列 第10项为24,第25项为
第10项为24,第25项为 ,
,
(1)求这个数列的通项公式;
(2)设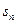 为其前n项和,求使
为其前n项和,求使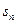 取最大值时的n值。
取最大值时的n值。
(本小题满分14分)
已知数列 满足
满足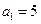 ,
, 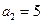 ,
,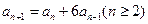 .
.
(1)求证: 是等比数列
是等比数列
(2)求数列 的通项公式
的通项公式
(3)设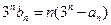 ,且
,且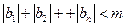 对于
对于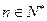 恒成立,求
恒成立,求 的取值范围
的取值范围
本小题满分14分)已知平面区域D由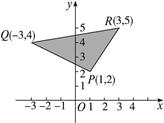
以P(1,2)、R(3,5)、Q(-3,4)为顶点的
三角形内部和边界组成
(1)写出表示区域D的不等式组
(2)设点(x,y)在区域D内变动,求目标函数
Z=2x+y的最小值;
(3)若在区域D内有无穷多个点(x,y)可使目标函数 取得最小值,求m的值。
取得最小值,求m的值。