(本小题满分12分)已知数列{an}的前n项和为Sn,点(n,Sn)(n∈N+)在函数f(x)=3x2-2x的图象上.
(1)求数列{an}的通项公式;
(2)设bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
如图五面体中,四边形ABCD是矩形,DA⊥平面ABEF,AB∥EF,AB=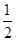 EF=2
EF=2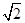 ,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.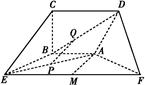
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面ADF.
如图,四棱锥S ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的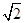 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.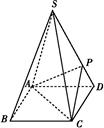
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P AC
AC D的大小;
D的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值;若不存在,试说明理由.
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.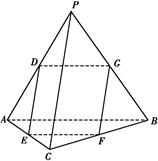
(1)求证:DE∥平面BCP.
(2)求证:四边形DEFG为矩形.
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.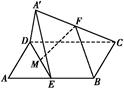
(1)求证:BF∥平面A′DE;
(2)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,EF∥AC,AB=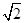 ,CE=EF=1.
,CE=EF=1.
(1)求证:AF∥平面BDE;
(2)求证:CF⊥平面BDE.