如图,四棱锥S ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的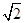 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.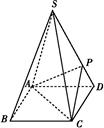
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P AC
AC D的大小;
D的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值;若不存在,试说明理由.
等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式;
(2)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
是否存在实数a,使得函数y=sin2x+a·cos x+a-在闭区间上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由
求函数y=sin4x+2sin xcos x-cos 4x的最小正周期和最小值;并写出该函数在[0,π]上的单调递增区间
设f(x)=6cos2x-sin 2x.
(1)求f(x)的最大值及最小正周期;
(2)若锐角α满足f(α)=3-2,求tanα的值
已知cos=,cos=-,且π<α+β<2π,<α-β<π,分别求cos 2α和cos 2β的值