如图五面体中,四边形ABCD是矩形,DA⊥平面ABEF,AB∥EF,AB=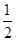 EF=2
EF=2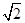 ,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.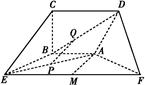
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面ADF.
(12分)
在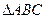 中,
中,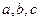 分别是
分别是 的对边长,已知
的对边长,已知 .
.
(1)若 ,求实数
,求实数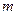 的值;
的值;
(2)若 ,求
,求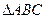 面积的最大值.
面积的最大值.
( 12分)已知函数f(x)=ax3+bx2的图象经过点M(1,4),曲线在点M处的切线恰好与直线x+9y=0垂直。
(1)求实数a、b的值;(2)若函数f(x)在区间[m,m+1]上单调递增,求m的取值范围.
(12分)已知函数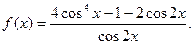
(1)求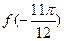 的值;
的值;
(2)当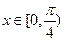 时,求
时,求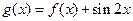 的最大值和最小值。
的最大值和最小值。
(本小题满分10分)
已知函数 ,当点(x,y) 是函数y = f (x) 图象上的点时,点
,当点(x,y) 是函数y = f (x) 图象上的点时,点 是函数y = g(x) 图象上的点.
是函数y = g(x) 图象上的点.
(1)写出函数y = g (x) 的表达式;
(2)当g(x)-f (x) 0时,求x的取值范围;
0时,求x的取值范围;
(3)当x在(2) 所给范围内取值时,求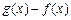 的最大值.
的最大值.
(本小题满分10分)
判断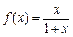 (x∈[0,3])的单调性,并证明你的结论.
(x∈[0,3])的单调性,并证明你的结论.