（本小题满分10分）选修4-4：极坐标与参数方程
在直角坐标系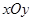
中，曲线C1的参数方程为
为参数），P为C1上的动点，Q为线段OP的中点．
（Ⅰ）求点Q的轨迹C2的方程；
（Ⅱ）在以O为极点，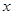
轴的正半轴为极轴（两坐标系取相同的长度单位）的极坐标系中，N为曲
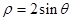上的动点，M为C2与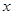轴的交点，求|MN|的最大值．
如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱
,
,底面
为直角梯形，其中BC∥AD, AB⊥AD, 
,O为AD中点.
(1)求直线
与平面
所成角的余弦值;
(2)求
点到平面
的距离
(3)线段
上是否存在点
,使得二面角
的余弦值为
?若存在,求出
的值;若不存在,请说明理由.
（本小题满分12分）
设函数
.
（Ⅰ）解不等式
；
（Ⅱ）对于实数
，若
，求证
．
题满分12分）
.如图，平行六面体ABCD－A1B1C1D1中，∠BAD＝∠BAA1＝∠DAA1＝60°，
（1）当AA1＝3，AB＝2，AD＝2，求AC1的长；
（2）当底面ABCD是菱形时，求证：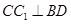
（本小题满分12分）
设命题
：方程
表示焦点在坐标轴上的双曲线，命题
：
。
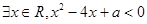（1）写出命题的否定；
（2）若“或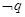
”为真命题，求实数
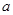的取值范围。
（本小题满分12分）
如图，一种电影放映灯的反射镜面是旋转椭圆面的一部分．
过对称轴的截口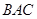
是椭圆的一部分，灯丝位于椭圆的一个焦点
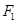上，片门位于另一个焦点
上，由椭圆一个焦点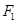发出的光线，经过旋转椭圆面反射后集中到另一个焦点．已知
，
，
试建立适当的坐标系，求截口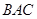所在椭圆的方程．