在等差数列{an}中,公差d=2,a2是a1与a4的等比中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ,数列
,数列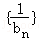 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.
已知在等比数列{an}中,a1=1,且a2是a1和a3﹣1的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=2n﹣1+an(n∈N*),求{bn}的前n项和Sn.
已知椭圆C的中心O为坐标原点,右焦点为F(1,0),A、B分别是椭圆C的左右顶点,P是椭圆C上的动点.
(Ⅰ)若△PAB面积的最大值为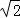 ,求椭圆C的方程;
,求椭圆C的方程;
(Ⅱ)过右焦点F做长轴AB的垂线,交椭圆C于M、N两点,若|MN|=3,求椭圆C的离心率.
下列命题中为真命题的是()
| A.命题“若x>1,则x2>1”的否命题 |
| B.命题“若x>y,则|x|>y”的逆命题 |
C.若k<5,则两椭圆 与 与 有不同的焦点 有不同的焦点 |
| D.命题“若方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围为(0,1)”的逆否命题 |
已知函数f(x)=alnx+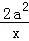 +x(a≠0).
+x(a≠0).
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与直线x﹣2y=0垂直,求实数a的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)当a∈(﹣∞,0)时,记函数f(x)的最小值为g(a),求证:g(a)≤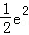 .
.