一个袋中有红、白两种球各若干个,现从中一次性摸出两个球,假设摸出的两个球至少有一个红球的概率为 ,至少一个白球的概率为
,至少一个白球的概率为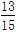 ,求摸出的两个球恰好红球白球各一个的概率.
,求摸出的两个球恰好红球白球各一个的概率.
如图,在四棱锥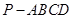 中,四边形
中,四边形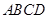 是正方形,
是正方形,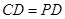 ,
,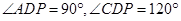 ,
,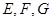 分别为
分别为 的中点.
的中点.
(Ⅰ)求证:平面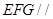 平面
平面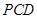 ;
;
(Ⅱ)求二面角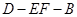 的平面角的大小.
的平面角的大小.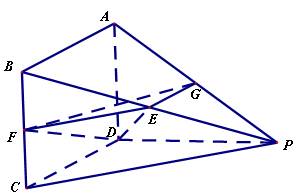
数列{an}中,an>0,an≠1,且 (n∈N*).
(n∈N*).
(1)证明:an≠an+1;
(2)若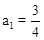 ,计算a2,a3,a4的值,并求出数列{an}的通项公式.
,计算a2,a3,a4的值,并求出数列{an}的通项公式.
已知函数 (
(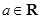 ,
,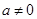 ),
),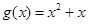 .
.
(1)求函数 的单调区间,并确定其零点个数;
的单调区间,并确定其零点个数;
(2)若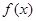 在其定义域内单调递增,求
在其定义域内单调递增,求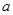 的取值范围;
的取值范围;
(3)证明不等式 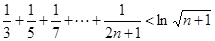 (
( ).
).
已知二次函数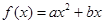 +
+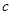 的图象通过原点,对称轴为
的图象通过原点,对称轴为 ,
,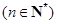 .
.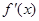 是
是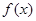 的导函数,且
的导函数,且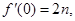
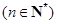 .
.
(1)求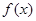 的表达式(含有字母
的表达式(含有字母 );
);
(2)若数列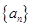 满足
满足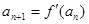 ,且
,且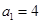 ,求数列
,求数列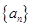 的通项公式;
的通项公式;
(3)在(2)条件下,若 ,
,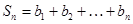 ,是否存在自然数
,是否存在自然数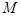 ,使得当
,使得当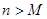 时
时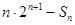
 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的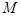 ;若不存在,说明理由.
;若不存在,说明理由.
已知椭圆 过
过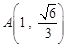 和点
和点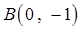 .
.
(1)求椭圆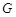 的方程;
的方程;
(2)设过点 的直线
的直线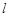 与椭圆
与椭圆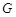 交于
交于 两点,且
两点,且 ,求直线
,求直线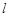 的方程.
的方程.