我市某中学举行“中国梦!校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两队各选出的5名选手的决赛成绩如图.
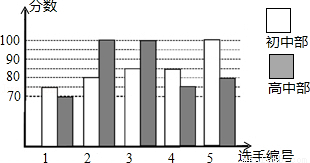
(1)根据图示填写下表;
| |
平均数 |
中位数 |
众数 |
| 初中部 |
? |
85 |
? |
| 高中部 |
85 |
? |
100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
如图,在平行四边形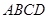 中,以点
中,以点 为圆心,
为圆心, 为半径的圆,交
为半径的圆,交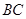 于点
于点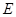 .
.
(1)求证: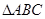 ≌
≌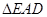 ;
;
(2)如果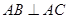 ,
,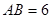 ,
,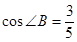 ,求
,求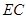 的长.
的长.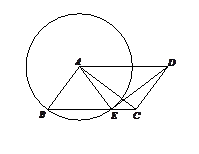
解方程: .
.
已知:如图,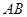 ⊥
⊥ ,
,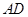 ∥
∥ ,
,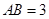 ,
, .点
.点 在线段
在线段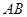 上,联结
上,联结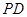 ,过点
,过点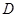 作
作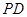 的垂线,与
的垂线,与 相交于点
相交于点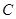 .设线段
.设线段 的长为
的长为 .
.
(1)当 时,求线段
时,求线段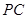 的长;
的长;
(2)设△ 的面积为
的面积为 ,求
,求 关于
关于 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当△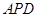 ∽△
∽△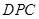 时,求线段
时,求线段 的长.
的长.

已知:如图,抛物线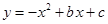 与
与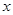 轴的负半轴相交于点
轴的负半轴相交于点 ,与
,与 轴相交于点
轴相交于点 (0,3),且∠
(0,3),且∠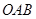 的余切值为
的余切值为 .
.
(1)求该抛物线的表达式,并写出顶点 的坐标;
的坐标;
(2)设该抛物线的对称轴为直线 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,
,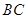 与直线
与直线 相交于点
相交于点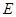 .点
.点 在直线
在直线 上,如果点
上,如果点 是△
是△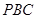 的重心,求点
的重心,求点 的坐标;
的坐标;
(3)在(2)的条件下,将(1)所求得的抛物线沿 轴向上或向下平移后顶点为点
轴向上或向下平移后顶点为点 ,写出平移后抛物线的表达式.点
,写出平移后抛物线的表达式.点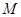 在平移后的抛物线上,且△
在平移后的抛物线上,且△ 的面积等于△
的面积等于△ 的面积的2倍,求点
的面积的2倍,求点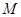 的坐标.
的坐标.
已知:如图,在梯形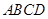 中,
中,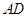 ∥
∥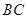 ,点
,点 、
、 在边
在边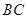 上,
上,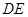 ∥
∥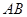 ,
,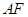 ∥
∥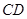 ,且四边形
,且四边形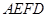 是平行四边形.
是平行四边形.
(1)试判断线段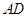 与
与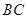 的长度之间有怎样的数量关系?并证明你的结论;
的长度之间有怎样的数量关系?并证明你的结论;
(2)现有三个论断:① ;②∠
;②∠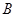 +∠
+∠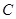 =90°;③∠
=90°;③∠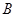 =2∠
=2∠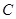 .请从上述三个论断中选择一个论断作为条件,证明四边形
.请从上述三个论断中选择一个论断作为条件,证明四边形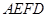 是菱形.
是菱形.