如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
小明、小华在一栋电梯楼前感慨楼房真高.小明说:“这楼起码20层!”小华却不以为然:“20层?我看没有,数数就知道了!”小明说:“有本事,你不用数也能明白!”小华想了想说:“没问题!让我们来量一量吧!”小明、小华在楼体两侧各选A、B两点,测量数据如图,其中矩形CDEF表示楼体,AB=150米,CD=10米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问: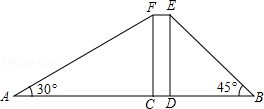
(1)楼高多少米?
(2)若每层楼按3米计算,你支持小明还是小华的观点呢?请说明理由.(参考数据: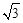 ≈1.73,
≈1.73, ≈1.41,
≈1.41,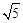 ≈2.24)
≈2.24)
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题: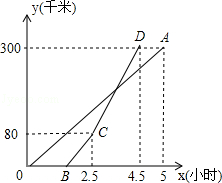
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“鄂”、“州”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“鄂”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明).
如图正方形ABCD的边长为4,E、F分别为DC、BC中点.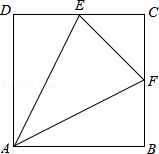
(1)求证:△ADE≌△ABF.
(2)求△AEF的面积.
先化简,后求值: ,其中a=3.
,其中a=3.