(本小题满分13分)已知函数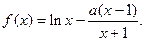 (
(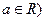
(1)若函数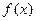 在定义域上为单调增函数,求
在定义域上为单调增函数,求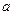 的取值范围;
的取值范围;
(2)设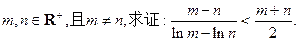
(本小题满分13分)已知函数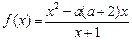 (
(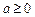 ).
).
(I)当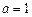 时,求
时,求 在点
在点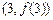 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在
在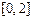 上的最小值.
上的最小值.
(本小题满分12分)某新型智能在线电池的电量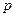 (单位:kwh)随时间
(单位:kwh)随时间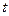 (单位:小时)的变化规律是:
(单位:小时)的变化规律是: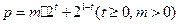 ,其中
,其中 是智能芯片实时控制的参数。
是智能芯片实时控制的参数。
(1)当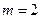 时,求经过多少时间电池电量是
时,求经过多少时间电池电量是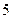 kwh;
kwh;
(2)如果电池的电量始终不低于2 kwh,求参数 的取值范围
的取值范围
(本小题满分13分)
设函数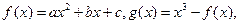 (
( )若
)若 上是增函数,在(0,1)上是减函数,函数
上是增函数,在(0,1)上是减函数,函数 在R上有三个零点,且1是其中一个零点。
在R上有三个零点,且1是其中一个零点。
(1)求b的值;
(2)求 最小值的取值范围。
最小值的取值范围。
(本小题满分12分)
已知命题 :方程
:方程 在
在 上有且仅有一解;命题
上有且仅有一解;命题 :只有一个实数
:只有一个实数 满足不等式
满足不等式 若命题
若命题 是假命题,求实数
是假命题,求实数 的取值范围.
的取值范围.