某校从参加某次知识竞赛的同学中,选取 名同学将其成绩(百分制,均为整数)分成
名同学将其成绩(百分制,均为整数)分成 ,
, ,
, ,
, ,
, ,
, 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
(1)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
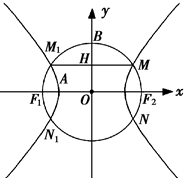
如图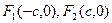 为双曲线
为双曲线 的两焦点,以
的两焦点,以 为直径的圆
为直径的圆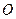 与双曲线
与双曲线 交于
交于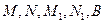 是圆
是圆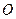 与
与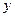 轴的交点,连接
轴的交点,连接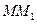 与
与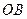 交于
交于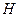 ,且
,且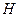 是
是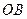 的中点,
的中点,
(1)当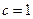 时,求双曲线
时,求双曲线 的方程;
的方程;
(2)试证:对任意的正实数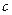 ,双曲线
,双曲线 的离心率为常数.
的离心率为常数.
由图看出显然一个交点,因此函数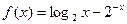 的零点个数只有一个
的零点个数只有一个
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲,
(1)根据以上的数据建立一个2×2的列联表;
(2)若认为“性别与患色盲有关系”,则出错的概率会是多少
19C.解:由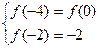 得
得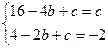 ,所以
,所以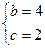 ,所以
,所以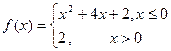 ,因为f(x)=x,所以
,因为f(x)=x,所以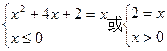 解得x=-1或-2或2,所以选C
解得x=-1或-2或2,所以选C
调查某医院某段时间内婴儿出生时间与性别的关系,得到以下数据。
| 晚上 |
白天 |
合计 |
|
| 男婴 |
24 |
31 |
55 |
| 女婴 |
8 |
26 |
34 |
| 合计 |
32 |
57 |
89 |
试问有多大把握认为婴儿的性别与出生时间有关系?
如何对语文、数学、英语、物理、化学、生物、地理、历史、政治这9门课程进行分类?
16.(2)解(1)当a=1,b=-2时,g(x)=f(x)-2,把f(x)图象向下平移两个单位就可得到g(x)图象,
这时函数g(x)只有两个零点,所以(1)不对
(2)若a=-1,-2<b<0,则把函数f(x)作关于x轴对称图象,然后向下平移不超过2个单位就可得到g(x)图象,这时g(x)有超过2的零点
(3)当a<0时, y=af(x)根据定义可断定是奇函数,如果b≠0,把奇函数y=af(x)图象再向上(或向下)平移后才是y=g(x)=af(x)+b的图象,那么肯定不会再关于原点对称了,肯定不是奇函数;当b=0时才是奇函数,所以(3)不对。所以正确的只有(2)
为了考察高中生学习语文与数学之间的关系,在某中学学生中随机地抽取了610名学生得到如下列表:
 语文 语文数学 |
及格 |
不及格 |
总计 |
| 及格 |
310 |
142 |
452 |
| 不及格 |
94 |
64 |
158 |
| 总计 |
404 |
206 |
610 |
由表中数据计算及 的观测值
的观测值 问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?
问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?