(本小题满分14分)
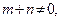 直线
直线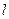 是线段
是线段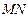 的垂直平分线.设椭圆E的方程为
的垂直平分线.设椭圆E的方程为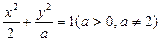 .
.
(1)当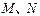 在
在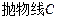 上移动时,求直线
上移动时,求直线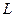 斜率
斜率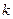 的取值范围;
的取值范围;
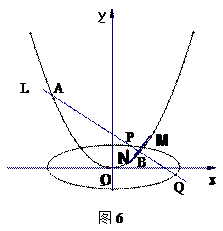
(2)已知直线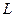 与抛物线
与抛物线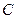 交于A、B两个不同点,
交于A、B两个不同点, 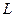 与椭圆
与椭圆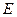 交于P、Q两个不同点,设AB中点为
交于P、Q两个不同点,设AB中点为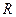 ,OP中点为
,OP中点为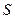 ,若
,若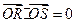 ,求椭圆
,求椭圆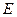 离心率的范围。
离心率的范围。
(本小题满分15分)
如图5,在底面为直角梯形的四棱锥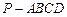
 中,
中,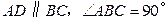 ,
, .
.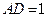 ,
,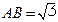 ,
,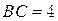 .
.
(1)求证: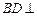
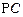 ;
;
(2)求直线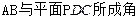 ;
;
(3)设点E在棱PC上,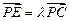 ,若
,若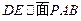 ,求
,求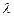 的值。
的值。
(本小题满分14分)
某商场“十.一”期间举行有奖促销活动,顾客只要在商店购物满800元就能得到一次摸奖机会.摸奖规则是:在盒子内预先放有5个相同的球,其中一个球标号是0,两个球标号都是40,还有两个球没有标号。顾客依次从盒子里摸球,每次摸一个球(不放回),若累计摸到两个没有标号的球就停止摸球,否则将盒子内球摸完才停止.奖金数为摸出球的标号 之和(单位:元),已知某顾客得到一次摸奖机会。
之和(单位:元),已知某顾客得到一次摸奖机会。
(1)求该顾客摸三次球被停止的概率;
(2)设 (元)为该顾客摸球停止时所得的奖金数,求
(元)为该顾客摸球停止时所得的奖金数,求 的分布列及数学期望
的分布列及数学期望 .
.
(本小题满分14分)
如图,在平面直角坐标系中,锐角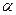 和钝角
和钝角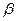 的终边分别与单位圆交于
的终边分别与单位圆交于 ,
,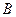 两点.
两点.
(1)如果 ,
,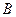 两点的纵坐标分别为
两点的纵坐标分别为 ,
, ,求
,求 和
和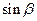
(2)在(Ⅰ)的条件下,求 的值;
的值;
(3)已知点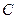
 ,求函数
,求函数 的值域.
的值域.
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?