如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
计算: .
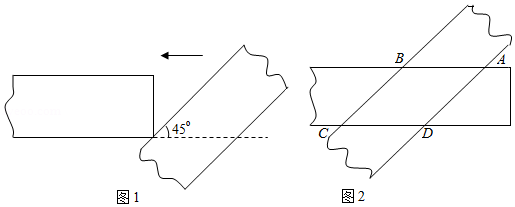
某校开展了一次综合实践活动,参加该活动的每个学生持有两张宽为 ,长足够的矩形纸条.探究两张纸条叠放在一起,重叠部分的形状和面积.
如图1所示,一张纸条水平放置不动,另一张纸条与它成 的角,将该纸条从右往左平移.
(1)写出在平移过程中,重叠部分可能出现的形状.
(2)当重叠部分的形状为如图2所示的四边形 时,求证:四边形 是菱形.
(3)设平移的距离为 ,两张纸条重叠部分的面积为 .求 与 的函数关系式,并求 的最大值.
在平面直角坐标系 中,等腰直角 的直角顶点 在 轴上,另两个顶点 , 在 轴上,且 ,抛物线经过 , , 三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线 交抛物线于 , 两点,如图2所示.
①求 面积的最小值.
②已知 是抛物线上一定点,问抛物线上是否存在点 ,使得点 与点 关于直线 对称,若存在,求出点 的坐标及直线 的一次函数表达式;若不存在,请说明理由.

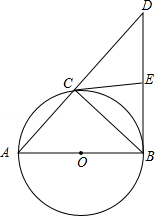
如图, 内接于 , 是 的直径, 与 相切于点 , 交 的延长线于点 , 为 的中点,连接 .
(1)求证: 是 的切线.
(2)已知 , ,求 , 两点之间的距离.
某药店在今年3月份,购进了一批口罩,这批口罩包括有一次性医用外科口罩和 口罩,且两种口罩的只数相同.其中购进一次性医用外科口罩花费1600元, 口罩花费9600元.已知购进一次性医用外科口罩的单价比 口罩的单价少10元.
(1)求该药店购进的一次性医用外科口罩和 口罩的单价各是多少元?
(2)该药店计划再次购进两种口罩共2000只,预算购进的总费用不超过1万元,问至少购进一次性医用外科口罩多少只?