在平面直角坐标系 中,等腰直角 的直角顶点 在 轴上,另两个顶点 , 在 轴上,且 ,抛物线经过 , , 三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线 交抛物线于 , 两点,如图2所示.
①求 面积的最小值.
②已知 是抛物线上一定点,问抛物线上是否存在点 ,使得点 与点 关于直线 对称,若存在,求出点 的坐标及直线 的一次函数表达式;若不存在,请说明理由.

如图,将平行四边形ABCD的边DC延长至点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)连接AC、BE,则当∠AFC与∠D满足什么条件时,四边形ABEC是矩形?请说明理由.
如图,已知A(a,m)、B(2a,n)是反比例函数y= (k>0)与一次函数y=-
(k>0)与一次函数y=- x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
如图,已知菱形AOBD的A、B、D三点在⊙O上,延长BO至点P,交⊙O于点C,且BP=3OB.
求证:AP是⊙O的切线.
为了预防流感,学校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y与x成反比(如图),现测得药物10min燃烧完,此时,教室内每立方米空气含药量为16mg.已知每立方米空气中含药量低于4mg时对人体无害,那么从消毒开始经多长时间后学生才能进教室?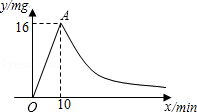
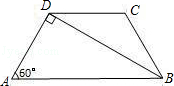
如图,在梯形ABCD中,AB∥CD,BD⊥AD,BC=CD,∠A=60°,CD=2cm.
(1)求∠CBD的度数;
(2)求下底AB的长.