2015年,号称“千湖之省”的湖北正遭受大旱,为提高学生的环保意识,节约用水,某校数学教师编造了一道应用题:为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水的收费作如下规定:
| 月用水量(单位:吨) |
单价(单位:元/吨) |
| 不大于6吨部分 |
2 |
| 大于6吨且不大于10吨部分 |
4 |
| 大于10吨部分 |
8 |
如某居民一月份用水9吨,则应收水费为:6×2+4×(9-6)=24(元)
(1)若该户居民3月份用水13吨,则应收水费 元.
(2)若该户居民5、6月份共用水15吨(五月份用水超过六月份),共交水费44元,则该户居民5、6月份各用水多少吨?
有序数对(m,n)中的整数m,n满足m-n=-6,且点P(m,n)在第二象限,写出所有符合条件的数对.
如图所示的平面直角坐标系中,写出点A,B,C,D,E,F,O各点的坐标.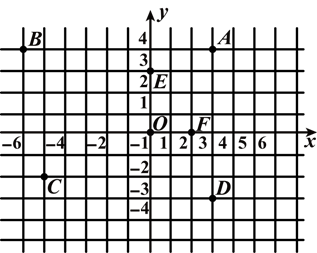
国际象棋、中国象棋和围棋号称世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置;
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
下表是用电脑中Excel(电子表格)制作的学生成绩档案的一部分.中间工作区被分成若干单元格,单元格用它所在列的英文字母和所在行的数字表示.如“余天泽”所在的单元格表示为A2.
(1)C4单元格中的内容是什么?表中“88”所在的单元格怎样表示?
(2)SUM(B2︰B4)表示对单元格B2至B4内的数据求和.那SUM(B3︰D3)表示什么?其结果是多少?
| A |
B |
C |
D |
… |
|
| 1 |
姓名 |
语文 |
数学 |
英语 |
… |
| 2 |
余天泽 |
99 |
100 |
93 |
… |
| 3 |
陈晨 |
82 |
96 |
88 |
… |
| 4 |
江阳 |
86 |
91 |
82 |
… |
如图是七年级(3)班部分学生的座次表,你能用有序数对表示这些同学的座位情况吗?试试看.