(本小题满分5分)解方程:  .
.
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,
与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移 ,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?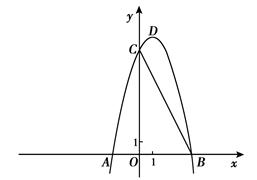
等边△ABC边长为6,P为BC边上一点,∠MPN=60°,且PM、PN分别 于边
于边
AB、AC交于点E、F.
(1)如图1,当点P为BC的三等分点,且PE⊥AB时,判断△EPF的形状;
(2)如图 2,若点P在BC边上运动,且保持PE⊥AB,设BP=x,四边形AEPF面积的y,求y与x的函数关系式,并写出自变量x的取值范围;
2,若点P在BC边上运动,且保持PE⊥AB,设BP=x,四边形AEPF面积的y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)如图3,若点P在BC边上运动,且∠MPN绕点P旋转,当CF=AE=2时,求PE的长.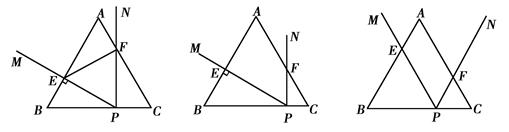
已知关于x的方程(m-1)x2-(2m-1)x+2=0有两个正整数根.
(1) 确定整数m值;
(2) 在(1)的条件下,利用图象写出方程(m-1)x2-(2m-1)x+2+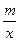 =0的实数根的个数.
=0的实数根的个数.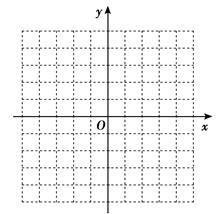
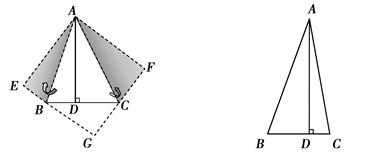
如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
(1)请你帮小萍求出x的值.
(2)参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)