图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了 层.将图1倒置后与原图拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层.将图1倒置后与原图拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为 …
… .
.

如果图1中的圆圈共有12层,
(1)当有12层时,图中共有 个圆圈;
(2)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数 ,…,则最底层最左边这个圆圈中的数是 ;
,…,则最底层最左边这个圆圈中的数是 ;
(3)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数 ,
, ,
, ,…,求图4中所有圆圈中各数之和.
,…,求图4中所有圆圈中各数之和.
如图,已知抛物线 (
( )的顶点坐标为(4,
)的顶点坐标为(4, ),且与y轴交于点C(0,2),与x轴交于A、B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A、B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小,若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C于点E、F,且CF=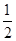 AC.
AC.
(1)求∠ACB的度数;
(2)若AC=8,求△ABF的面积.
如图,要在长32m,宽20m的长方形绿地上修建宽度相同的道路,六块绿地面积共570m,问道路宽应为多宽?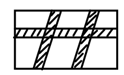
如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.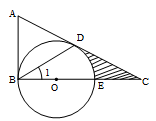
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
已知关于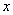 的一元二次方程
的一元二次方程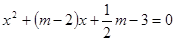 .
.
(1)求证:无论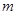 取什么实数值,这个方程总有两个不相等的实数根.
取什么实数值,这个方程总有两个不相等的实数根.
(2)若这个方程的两个实数根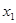 、
、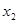 满足
满足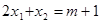 ,求
,求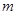 的值.
的值.