在平面直角坐标系中，△ABC的三个顶点位置如图所示．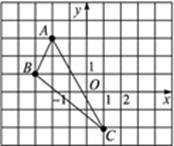
（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点）；
（2）直接写出△A′B′C′三点的坐标：A′_________，B′__________，C′_________．
（3）求A B′的长。
阅读下面材料：
小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA="3" ，PB=4，PC=5，求∠APB的度数.
小伟是这样思考的：如图2，利用旋转和全等的知识构造△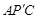
，连接
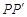，得到两个特殊的三角形，从而将问题解决．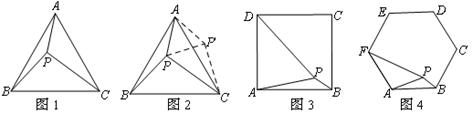
请你回答：图1中∠APB的度数等于 .
参考小伟同学思考问题的方法，解决下列问题：
（1）如图3，在正方形ABCD内有一点P，且PA=
，PB=1，PD=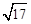
，则∠APB的度数等于，正方形的边长为；
（2）如图4，在正六边形ABCDEF内有一点P，且PA=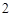
，PB=1，PF=
，则∠APB的度数等于，正六边形的边长为．
在矩形ABCD中，点O在对角线BD上，以OD为半径的⊙O与AD、BD分别交于点E、F，且∠ABE=∠DBC.
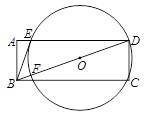
（1）求证：BE与⊙O相切；
（2）若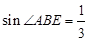
，CD=2，求⊙O的半径.
如图，在Rt△ABC中，∠CAB=90°，AD是∠CAB的平分线，tanB=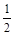
，求
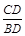的值．
如图，AB为⊙O的直径，直线DT切⊙O于T，AD⊥DT于D，交⊙O于点C，AC=2，DT =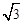
，求∠ABT的度数.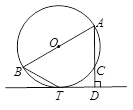 
二次函数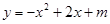
的图象与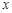
轴的一个交点为A
，另一个交点为B，与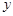
轴交于点C.
（1）求
的值及点B、点C的坐标；
（2）直接写出当
时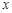，的取值范围；
（3）直接写出当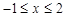
时，
的取值范围．