在矩形ABCD中,点O在对角线BD上,以OD为半径的⊙O与AD、BD分别交于点E、F,且∠ABE=∠DBC.
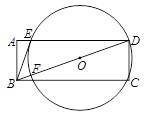
(1)求证:BE与⊙O相切;
(2)若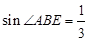 ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍 从学校出发.苏老师因有事情, 从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
密码锁有三个转轮,每个转轮上有十个数字:0,1,2, .小黄同学是9月份中旬出生,用生日“月份 日期”设置密码:
小张同学要破解其密码:
(1)第一个转轮设置的数字是9,第二个转轮设置的数字可能是 .
(2)请你帮小张同学列举出所有可能的密码,并求密码数能被3整除的概率;
(3)小张同学是6月份出生,根据(1)(2)的规律,请你推算用小张生日设置的密码的所有可能个数.
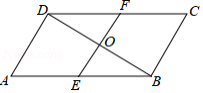
平行四边形 中, , , 的中垂线分别交 , 于点 , ,垂足为 .
(1)求证: ;
(2)若 ,求 的值.
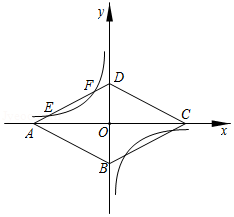
如图,已知菱形 的对称中心是坐标原点 ,四个顶点都在坐标轴上,反比例函数 的图象与 边交于 , 两点.
(1)求 , 的值;
(2)写出函数 图象在菱形 内 的取值范围.
请完成如下探究系列的有关问题:
探究1:如图1, 是等腰直角三角形, ,点 为 上一动点,连接 ,以 为边在 的右侧作正方形 ,连接 ,则线段 , 之间的位置关系为 ,数量关系为 .
探究2:如图2,当点 运动到线段 的延长线上,其余条件不变,探究1中的两条结论是否仍然成立?为什么?(请写出证明过程)
探究3:如图3,如果 , , 仍然保留为 ,点 在线段 上运动,请你判断线段 , 之间的位置关系,并说明理由.
