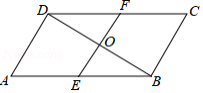
平行四边形 中, , , 的中垂线分别交 , 于点 , ,垂足为 .
(1)求证: ;
(2)若 ,求 的值.
如图,已知△ABC的三个顶点在格点上.
(1)△ABC的三边中长度为 的边为__________;
的边为__________;
(2)作出与△ABC关于x轴对称的△A1B1C1;
(3)写出下列点的坐标:A1(______,_______)B1(_______,_______)C1(_______,_______).
如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.求证:MD=ME.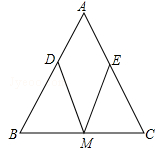
如图,已知:大风把一颗大树刮断,折断的一端恰好落在地面上的A处,量得BC=6m,AC=8m,试计算这棵大树的高度. 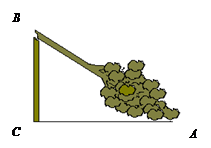
如图,抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,且交y轴于点C,对称轴与抛物线相交于点P、与直线BC相交于点M.
(1)求该抛物线的解析式.
(2)在抛物线上是否存在一点N,使得|MN-ON|的值最大?若存在,请求出点N的坐标;若不存在,请说明理由.
(3)连接PB,请探究:在抛物线上是否存在一点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
如图,已知☉O的直径AB=8,过A、B两点作☉O的切线AD、BC.
(1)当AD=2,BC=8时,连接OC、OD、CD.
①求△COD的面积.
②试判断直线CD与☉O的位置关系,并说明理由.
(2)若直线CD与☉O相切于点E,设AD=x(x>0),试用含x的式子表示四边形ABCD的面积S,并探索S是否存在最小值,写出探索过程.