如图,抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,且交y轴于点C,对称轴与抛物线相交于点P、与直线BC相交于点M.
(1)求该抛物线的解析式.
(2)在抛物线上是否存在一点N,使得|MN-ON|的值最大?若存在,请求出点N的坐标;若不存在,请说明理由.
(3)连接PB,请探究:在抛物线上是否存在一点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
解方程⑴


⑵

某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
| 运输工具 |
途中平均速度 (千米/时) |
运费 (元/千米) |
装卸费用 (元) |
| 火车 |
100 |
15 |
2000 |
| 汽车 |
80 |
20 |
900 |
(1)如果选择汽车的总费用比选择火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答。
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是A市水果批发部门的经理,要想将这种水果运往其他地区销售。你将选择哪种运输方式比较合算呢?
一列客车长200 m,一列货车长280 m,在平行的轨道上相向行驶,从两车头相遇到两车尾相离经过18s,已知客车与货车的速度之比是5∶3,问两车每秒各行驶多少米?
如图所示,已知 ,OM平分
,OM平分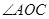 ,ON平分
,ON平分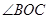 ;
;(1)求
 ;
;(2)
 ,求
,求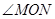 的度数。
的度数。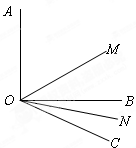
某车间有60名工人,生产一种螺栓和螺帽,平均每人每小时生产螺栓15个或螺帽10个,一个螺栓配两个螺帽。应分配多少人生产螺栓和螺帽,才能刚好配套?