已知抛物线y=ax2+2x+c与x轴交于A(1,0)和点B,与y轴交于点C(0,﹣3).
(1)求抛物线的解析式.
(2)如图1,已知点H的坐标为(0,1),设点M为y轴左侧抛物线上的一个动点,试猜想:是否存在这样的点M,使|MA﹣MH|的值最大,如果存在,请求出点M的坐标;如果不存在,请说明理由.
(3)如图2,过x轴上点E(﹣2,0)作ED⊥AB交抛物线于点D,在y轴上找一点F,使△EDF的周长最小,求出此时点F的坐标;
(4)如图3,已知点N(0,﹣1).问在抛物线上是否存在点Q(点Q在y轴的左侧),使得△QNC的面积与△QNA的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
如图,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证BD=AE;
(2)若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
先阅读,再回答问题:如图1,已知△ABC中,AD为中线.延长AD至E,使DE=AD.在△ABD和△ECD中,AD=DE,∠ADB=∠EDC,BD=CD,所以,△ABD≌△ECD(SAS),进一步可得到AB=CE,AB∥CE等结论.
在已知三角形的中线时,我们经常用“倍长中线”的辅助线来构造全等三角形,并进一步解决一些相关的计算或证明题.
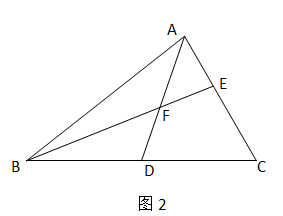
解决问题:如图2,在△ABC中,AD是三角形的中线,F为AD上一点,且BF=AC,连结并延长BF交AC于点E,求证:AE=EF.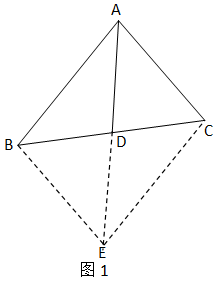
如图,△ABC中,AB=AC,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点.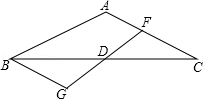
⑴求证:BG=CF
⑵请你判断AF、BG、AB之间的大小关系,并说明理由.
如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,求∠ADC的度数.
若 无意义,且
无意义,且 ,求
,求 的值.
的值.