如图，在平面直角坐标系中，将一块腰长为
的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，顶点A的坐标为
，点B在抛物线
上．
（1）直角顶点C的坐标为 ；
（2）求抛物线的解析式；
（3）若点D是（1）中所求抛物线在第三象限内的一个动点，连接BD、CD．当△BCD的面积最大时，求点D的坐标．
观察下列等式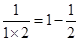
，
，
，
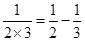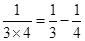将以上三个等式两边分别相加得：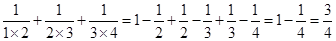
．
（1）猜想并写出：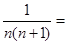
．
（2）根据以上规律直接写出下列各式的计算结果：
①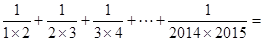
．
②
．
（3）探究并计算：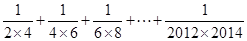
10袋小麦以每袋150千克为准，超过的千克数记为正数，不足的千克数记为负数，分别记为:-6、-3、-1、-2、+7、+3、+4、-3、-2、+1与标准质量相比较，这10袋小麦总计超过或不足多少千克？10袋小麦总质量是多少千克？每袋小麦的平均质量是多少千克？
若a、b互为相反数，c、d互为倒数，m的绝对值为2，求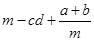
的值。
某公司去年1~3月平均每月亏损1．7万元，4~6月平均每月盈利1．8万元，7~10月平均每月盈利1．9万元，11、12月平均每月亏损2．5万元。问这个公司去年总的盈亏情况如何？
如图，蚂蚁在距巢穴2米远找到一只苍蝇，决定将其搬回家，可蚂蚁每一分钟内前进1米，却被风刮退2米，请问这只蚂蚁能否回到巢穴？如不能，请说明理由；如能，算一算何时能回巢穴．