(本题6分)已知关于x的方程x2-(k+1)x+ k2+1=0
k2+1=0
(1)k取什么值时,方程有两个实数根;
(2)如果方程有两个实数根x1、x2, =x2,求k的值.
=x2,求k的值.
(本题5分)已知a、b为方程x2-2x-1=0的两根,不解方程,求a2+2b2-2a-4b+3的值.
根据条件求下列抛物线的解析式:
(1)二次函数的图象经过(0,1),(2,1)和(3,4);
(2)抛物线的顶点坐标是(-2,1),且经过点(1,-2).
解方程(本题8分)
(1)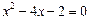 (2)
(2)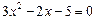
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴子点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3。
(1)设点P的纵坐标为p,写出p随k变化的函数关系式。
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明;
(3)是否存在使△AMN的面积等于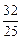 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。