某校高一年级甲、已两班准备联合举行晚会,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.甲班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时甲班代表获胜,否则乙班代表获胜.
(Ⅰ)根据这个游戏方案,转到的两数之和会出现哪些可能的情况?
(Ⅱ)游戏方案对双方是否公平?请说明理由.
设向量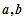 满足
满足
(1)求 的值;
的值;
(2)求 与
与 夹角的正弦值.
夹角的正弦值.
已知
(1)求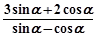 的值;
的值;
(2)求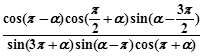 的值;
的值;
(3)若 是第三象限角,求
是第三象限角,求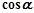 的值.
的值.
设 为平面内的四点,且
为平面内的四点,且
(1)若 求
求 点的坐标;
点的坐标;
(2)设向量 若
若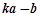 与
与 平行,求实数
平行,求实数 的值.
的值.
已知△ 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,
, ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(1)求顶点 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种圆锥曲线;
为何种圆锥曲线;
(2)当 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合), 试问:直线
不重合), 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
从某校高二年级 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组 ,第二组
,第二组 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
| 分组 |
频数 |
频率 |
频率/组距 |
 |
 |
 |
 |
 |
 |
 |
 |
频率分布直方图如下:
(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: 的事件的概率.
的事件的概率.