已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件:f(x﹣1)=f(3﹣x),且方程f(x)=2x有两等根.
(1)求f(x)的解析式.
(2)求f(x)在[0,t]上的最大值.
(3)是否存在实数m、n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],
如果存在,求出m、n的值,如果不存在,说明理由.
(本小题满分10分)选修4-1:几何证明选讲
如图,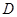 ,
, 分别为
分别为
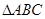 的边
的边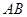 ,
,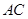 上的点,且不与
上的点,且不与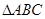 的顶点重合。已知
的顶点重合。已知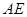 的长为m,
的长为m,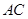 的长为n,AD,
的长为n,AD,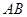 的长是关于
的长是关于 的方程
的方程 的两个根。
的两个根。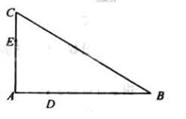
(1)证明: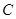 ,
,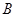 ,
,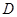 ,
, 四点共圆;
四点共圆;
(2)若 ,且
,且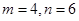 ,求
,求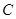 ,
,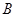 ,
,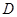 ,
, 所在圆的半径。
所在圆的半径。
(本小题满分12分)已知抛物线 ,直线
,直线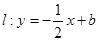 与抛物线交于
与抛物线交于 两点.
两点.
(1)若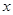 轴与以
轴与以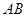 为直径的圆相切,求该圆的方程;
为直径的圆相切,求该圆的方程;
(2)若直线与 轴负半轴相交,求
轴负半轴相交,求 面积的最大值。
面积的最大值。
(本小题满分12分) 已知函数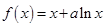 ,在
,在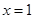 处的切线与直线
处的切线与直线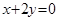 垂直,函数
垂直,函数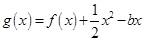
(1)求实数 的值;;
的值;;
(2)设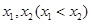 是函数
是函数 的两个极值点,若
的两个极值点,若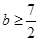 ,求
,求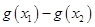 的最小值。
的最小值。
(本小题满分12分)如图,在斜三棱柱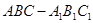 中,O是AC的中点,A1O⊥平面
中,O是AC的中点,A1O⊥平面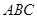 ,
,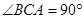 ,
,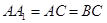 .
.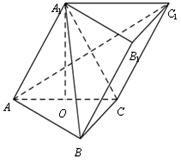
(1)求证: AC1⊥平面A1BC;
(2)若AA1=2,求点C到平面 的距离。
的距离。
(本小题满分12分)某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的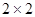 列联表,
列联表,
| 优秀 |
非优秀 |
合计 |
|
| 甲班 |
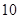 |
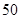 |
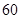 |
| 乙班 |
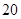 |
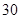 |
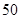 |
| 合计 |
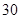 |
 |
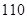 |
(1)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(2)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
参考公式与临界值表: .
.
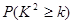 |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
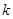 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |