某省2015年全省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5 cm之间,将测量结果按如下方式分成6组:第一组 [157.5,162.5),第二组[162.5,167.5),…,第6 组[182.5,187.5],下图是按上面分组方法得到的频率分布直方图.
(1)试评估我校高三年级男生在全省高中男生中的平均身高状况;
(2)求这50名男生身高在177.5cm以上(含177.5 cm)的人数;
(3)在这50名男生身高在177.5cm以上(含177.5cm)的人中任意抽取2人,该2人中身高排名(以高到低)在全省前130名的人数记为 ,求
,求 的数学期望.
的数学期望.
参考数据:若 ~
~ ,则
,则 ,
, ,
,
已知数列 满足
满足

(1)求
(2)设 求证:
求证: ;
;
(3)求数列 的通项公式。
的通项公式。
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD//BC且AD﹥BC,∠DAB=∠ABC=90°,PA= ,AB=BC=1。M为PC的中点。
,AB=BC=1。M为PC的中点。
(1)求二面角M—AD—C的大小;(6分)
(2)如果∠AMD=90°,求线段AD的长。
袋中有同样的球 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机且不返回地摸球,每次摸
个黄色,现从中随机且不返回地摸球,每次摸 个,当两种颜色的球都被摸到时,即停止摸球,记随机变量
个,当两种颜色的球都被摸到时,即停止摸球,记随机变量 为此时已摸球的次数,求:.
为此时已摸球的次数,求:.
(1)随机变量 的概率分布; (9分)
的概率分布; (9分)
(2)随机变量 的数学期望与方差.
的数学期望与方差.
(10分)已知: .
.
(1)求: 的取值范围;(5分)
的取值范围;(5分)
(2)求:函数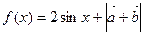 的最小值. (5分)
的最小值. (5分)
(本小题满分14分)
设二次函数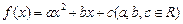 满足下列条件:
满足下列条件:
①当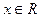 时,其最小值为0,且
时,其最小值为0,且 成立;
成立;
②当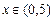 时,
时,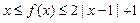 恒成立.
恒成立.
(1)求 的值;
的值;
(2)求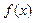 的解析式;
的解析式;
(3)求最大的实数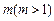 ,使得存在
,使得存在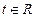 ,只要当
,只要当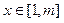 时,就有
时,就有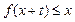 成立
成立