如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD//BC且AD﹥BC,∠DAB=∠ABC=90°,PA= ,AB=BC=1。M为PC的中点。
,AB=BC=1。M为PC的中点。
(1)求二面角M—AD—C的大小;(6分)
(2)如果∠AMD=90°,求线段AD的长。
(本小题满分13分)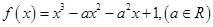 .
.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)若 的图像不存在与
的图像不存在与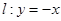 平行或重合的切线,求实数
平行或重合的切线,求实数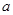 的取值范围.
的取值范围.
(本小题满分13分)
某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答下列问题: 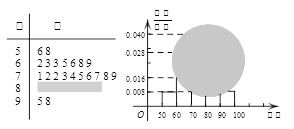
(Ⅰ)求全班人数及分数在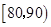 之间的频数;
之间的频数;
(Ⅱ)不看茎叶图中的具体分数,仅根据频率分布直方图估计该班的平均分数;
(Ⅲ)若要从分数在 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在 之间的概率.
之间的概率.
(本小题满分12分)
如图,四棱锥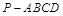 中,底面
中,底面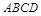 是菱形,
是菱形,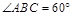 ,侧面
,侧面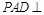 底面
底面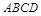 ,
,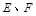 分别为
分别为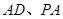 中点.
中点. 
(Ⅰ)求证: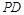 ∥平面
∥平面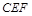 ;
;
(Ⅱ)求证:平面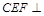 平面
平面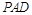 .
.
(本小题满分12分)设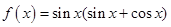 .
.
(Ⅰ)求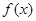 最大值及相应
最大值及相应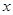 值;
值;
(Ⅱ)锐角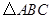 中,满足
中,满足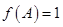 .求
.求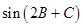 取值范围.
取值范围.
(本小题满分12分)
等差数列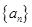 中,前
中,前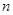 项和为
项和为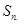 ,且
,且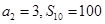 .
.
(Ⅰ)求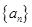 通项公式;
通项公式;
(Ⅱ)设 ,求数列
,求数列 前
前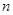 项的和
项的和 .
.