设椭圆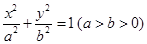 的左、右顶点分别为
的左、右顶点分别为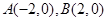 ,离心率
,离心率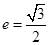 .过该椭圆上任一点
.过该椭圆上任一点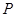 作
作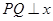 轴,垂足为
轴,垂足为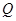 ,点
,点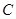 在
在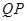 的延长线上,且
的延长线上,且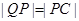 .
.
(1)求椭圆的方程;
(2)求动点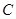 的轨迹
的轨迹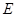 的方程;
的方程;
(3)设直线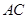 (
(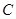 点不同于
点不同于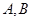 )与直线
)与直线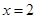 交于点
交于点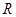 ,
,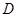 为线段
为线段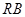 的中点,试判断直线
的中点,试判断直线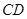 与曲线
与曲线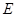 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
已知函数 ,
,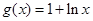 .
.
(Ⅰ)若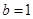 ,且
,且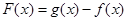 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(Ⅱ)设函数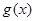 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点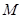 、
、 ,过线段
,过线段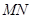 的中点
的中点 作
作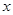 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 、
、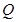 ,是否存在点
,是否存在点 ,使
,使 在点
在点 处的切线与
处的切线与 在点
在点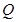 处的切线平行?如果存在,求出点
处的切线平行?如果存在,求出点 的横坐标,如果不存在,说明理由.
的横坐标,如果不存在,说明理由.
已知向量 ,且
,且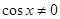 .
.
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)设 的内角
的内角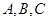 的对边分别为
的对边分别为 ,
, ,且
,且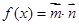 ,求函数
,求函数 的值域.
的值域.
如图,为对某失事客轮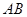 进行有效援助,现分别在河岸
进行有效援助,现分别在河岸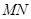 选择两处
选择两处 、
、 用强光柱进行辅助照明,其中
用强光柱进行辅助照明,其中 、
、 、
、 、
、 在同一平面内.现测得
在同一平面内.现测得 长为
长为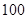 米,
米,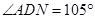 ,
, ,
,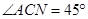 ,
,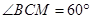 .
.
(1)求 的面积;
的面积;
(2)求船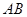 的长.
的长.
已知在锐角 中,
中, 为角
为角 所对的边,且
所对的边,且 .
.
(Ⅰ)求角 的值;
的值;
(2)若 ,且
,且 是锐角三角形,求
是锐角三角形,求 的取值范围.
的取值范围.
已知函数的最大值为2,是集合中的任意两个元素,且的最小值为.
(1)求函数的解析式及其对称轴;
(2)求在区间 的取值范围.
的取值范围.