已知向量 ,且
,且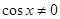 .
.
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)设 的内角
的内角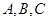 的对边分别为
的对边分别为 ,
, ,且
,且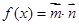 ,求函数
,求函数 的值域.
的值域.
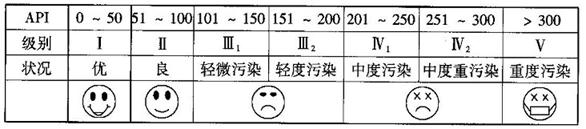
(本题12分)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间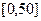 ,
,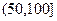 ,
,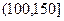 ,
, ,
,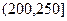 ,
,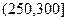 进行分组,得到频率分布直方图如图.
进行分组,得到频率分布直方图如图.
(1)求直方图中 的值;
的值;
(2)计算一年中空气质量为良的天数;
(3)某环保部门准备在一年内随机到该城市考察两次空气质量,求两次考察空气质量都为良的概率(结果用分数表示).
(本题12分)定义在R上的函数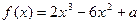 ,已知
,已知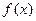 在
在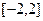 上有最小值3。
上有最小值3。
(1)求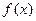 的单调区间;
的单调区间;
(2)求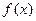 在
在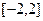 上的最大值。
上的最大值。
(本题12分)已知某种从太空带回的植物种子每粒成功发芽的概率都为 ,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
(1) 第一小组做了三次实验,求实验成功的平均次数;
(2) 第二小组连续进行实验,求实验首次成功时所需的实验次数的期望;
(3)两个小组分别进行2次试验,求至少有2次实验成功的概率.
(本大题满分14分)
函数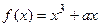 与
与 的图象有公共点
的图象有公共点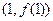 ,且它们的图象在该点处的切线相同。记
,且它们的图象在该点处的切线相同。记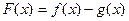 。
。
(Ⅰ)求 的表达式,并求
的表达式,并求 在
在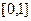 上的值域;
上的值域;
(Ⅱ)设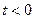 ,函数
,函数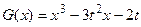 ,
,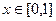 。若对于任意
。若对于任意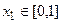 ,总存在
,总存在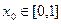 ,使得
,使得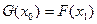 ,求实数
,求实数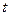 的取值范围。
的取值范围。
(本大题共13分)
已知函数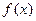 是定义在R的奇函数,当
是定义在R的奇函数,当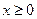 时,
时,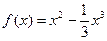 .
.
(1)求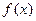 的表达式;
的表达式;
(2)讨论函数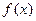 在区间
在区间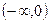 上的单调性;
上的单调性;
(3)设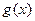 是函数
是函数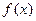 在区间
在区间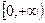 上的导函数,问是否存在实数
上的导函数,问是否存在实数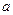 ,满足
,满足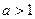 并且使
并且使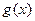 在区间
在区间 上的值域为
上的值域为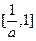 ,若存在,求出
,若存在,求出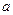 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。