(本题12分)已知某种从太空带回的植物种子每粒成功发芽的概率都为 ,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
,某植物研究所分两个小组分别独立开展该种子的发芽实验,每次实验种一粒种子,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.
(1) 第一小组做了三次实验,求实验成功的平均次数;
(2) 第二小组连续进行实验,求实验首次成功时所需的实验次数的期望;
(3)两个小组分别进行2次试验,求至少有2次实验成功的概率.
(本小题满分12分)
已知函数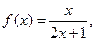 数列
数列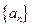 满足
满足 .
.
(1)求证:数列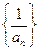 是等差数列;
是等差数列;
(2)若数列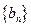 前
前 项和为
项和为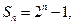 记
记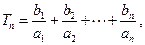 求
求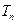 .
.
(本小题满分12分)
在海岸A处,发现北偏东 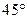 方向,距离A为
方向,距离A为 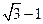
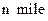 的B处有一艘走私船,在A处北偏西
的B处有一艘走私船,在A处北偏西 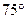 方向,距离A为
方向,距离A为 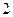
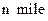 的C处有一艘缉私艇奉命以
的C处有一艘缉私艇奉命以 
 的速度追截走私船,此时,走私船正以
的速度追截走私船,此时,走私船正以 
 的速度从B处向北偏东
的速度从B处向北偏东 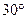 方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便)
方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便)
|
|
(本小题满分12分)
某汽车公司购买了4辆大客车,每辆200万元,用于长途客运,预计每辆车每年收入约100万元,每辆车每年各种费用约为16万元,且从第二年开始每年比上一年所需费用要增加16万元.
(1)写出4辆车运营的总利润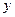 (万元)与运营年数
(万元)与运营年数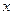
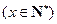 的函数关系式;
的函数关系式;
(2)这4辆车运营多少年,可使年平均运营利润最大?
(本小题满分12分)
在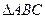 中,内角
中,内角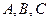 对边的边长分别是
对边的边长分别是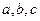 ,且
,且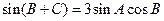 .
.
(1)求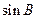 的值;
的值;
(2)若 ,且
,且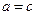 ,求
,求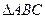 的面积.
的面积.
(本小题满分12分)
解关于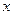 的不等式:
的不等式: .
.