已知椭圆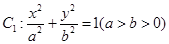 的右焦点与抛物线
的右焦点与抛物线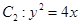 的焦点F重合,椭圆
的焦点F重合,椭圆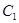 与抛物线
与抛物线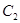 在第一象限的交点为P,
在第一象限的交点为P, .
.
(1)求椭圆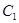 的方程;
的方程;
(2)过点A(-1,0)的直线与椭圆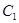 相交于M,N两点,求使
相交于M,N两点,求使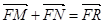 成立的动点R的轨迹方程.
成立的动点R的轨迹方程.
(本小题满分12分)已知函数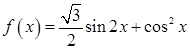
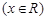 .
.
(Ⅰ)求函数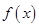 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)求函数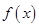 在区间
在区间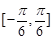 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)已知关于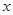 的不等式
的不等式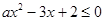 的解集为
的解集为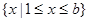 .
.
(1)求实数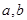 的值;
的值;
(2)解关于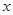 的不等式:
的不等式: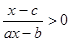 (
(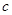 为常数)
为常数)
(本小题满分12分)某单位建造一间背面靠墙的小房,地面面积为12 m2,房屋正面每平方米的造价为1200元,房屋侧面每平方米的造价为800元,屋顶的造价为5800元.如果墙高为3 m,且不计房屋背面和地面的费用,问怎样设计房屋能使总造价最低?最低总造价是多少?
(本小题满分12分)等比数列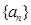 中,已知
中,已知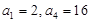
(Ⅰ)求数列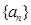 的通项公式
的通项公式
(Ⅱ)若 分别为等差数列
分别为等差数列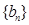 的第3项和第5项,试求数列
的第3项和第5项,试求数列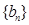 的通项公式及前
的通项公式及前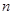 项和
项和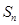
(本小题满分12分)在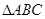 中,
中,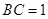 ,
,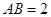 ,
,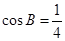 ,
,
(1)求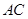 ;
;
(2)求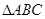 的面积.
的面积.