(1)用分数指数幂表示下式 (a>0,b>0)
(a>0,b>0)
(2)计算:
(本小题满分12分)数列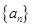 满足
满足 ,
,
设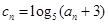 .
.
(Ⅰ)求证: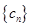 是等比数列;
是等比数列;
(Ⅱ)求数列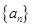 的通项公式;
的通项公式;
(Ⅲ)设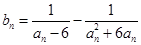 ,数列
,数列 的前
的前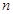 项和为
项和为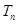 ,求证:
,求证: .
.
(本小题满分12分)如图,在三棱台 中,
中, 分别为
分别为 的中点.
的中点.
(Ⅰ)求证: 平面
平面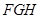 ;
;
(Ⅱ)若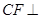 平面
平面 ,
,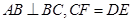 ,
,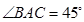 ,求平面
,求平面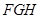 与平面
与平面 所成角(锐角)的大小.
所成角(锐角)的大小.
(本小题满分12分)如图,在平面直角坐标系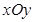 中,点
中,点 ,直线
,直线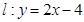 ,设圆
,设圆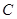 的半径为
的半径为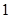 ,圆心在
,圆心在 上.
上.
(Ⅰ)若圆心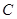 也在直线
也在直线 上,过点
上,过点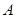 作圆
作圆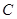 的切线,求切线的方程;
的切线,求切线的方程;
(Ⅱ)若圆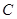 上存在点
上存在点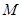 ,使
,使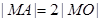 ,求圆心
,求圆心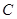 的横坐标
的横坐标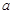 的取值范围.
的取值范围.
(本小题满分12分)如图,四面体 中,
中,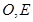 分别
分别 的中点,
的中点,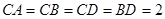 ,
, .
.
(Ⅰ)求证:AO⊥平面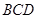 ;
;
(Ⅱ)求异面直线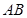 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离.
(本小题满分12分)设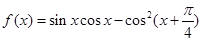 .
.
(Ⅰ)求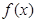 的单调区间;
的单调区间;
(Ⅱ)在锐角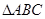 中,角
中,角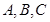 的对边分别为
的对边分别为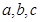 ,若
,若 ,求
,求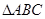 面积的最大值.
面积的最大值.