已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设 ,过点
,过点 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆
交椭圆 于
于 两点,连接
两点,连接 分别交直线
分别交直线 于
于 两点,若直线
两点,若直线 的斜率分别为
的斜率分别为 ,试问:
,试问: 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
已知圆方程为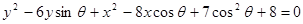 .
.
(1)求圆心轨迹的参数方程C;
(2)点 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求 的取值范围.
的取值范围.
(本题14分)如图,一水渠的横断面是抛物线形,O是抛物线的顶点,口宽EF=4米,高3米,建立适当的直角坐标系,(1)求抛物线方程.(2)若将水渠横断面改造成等腰梯形ABCD,要求高度不变,只挖土,不填土,求梯形ABCD的下底AB多大时,所挖的土最少? 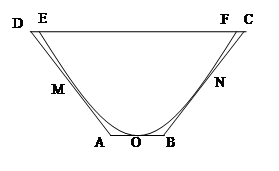
(本题12分)直线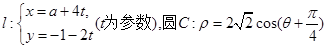 (极轴与x轴的非负半轴重合,且单位长度相同)。
(极轴与x轴的非负半轴重合,且单位长度相同)。
(1)求圆心C到直线 的距离;(2)若直线
的距离;(2)若直线 被圆C截的弦长为
被圆C截的弦长为 的值。
的值。
(本题12分) 某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .若备选的5个居民小区中有三个非低碳小区,两个低碳小区.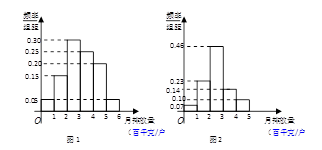
(1)求所选的两个小区恰有一个为“非低碳小区”的概率;
(2)假定选择的“非低碳小区”为小区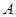 ,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区
,调查显示其“低碳族”的比例为1:2,数据如图1所示,经过大力宣传,三个月后又进行一次调查,数据如图2所示,问这时小区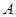 是否达到“低碳小区”的标准?
是否达到“低碳小区”的标准?
(本题12分)已知曲线y=
(1)求曲线在x=2处的切线方程;(2)求曲线过点(2,4)的切线方程.