（本题12分）
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查，以计算每户的碳月排放量．若月排放量符合低碳标准的称为“低碳族”，否则称为“非低碳族”．若小区内有至少
的住户属于“低碳族”，则称这个小区为“低碳小区”，否则称为“非低碳小区” ．若备选的5个居民小区中有三个非低碳小区，两个低碳小区.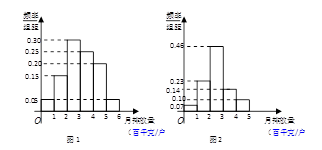
（1）求所选的两个小区恰有一个为“非低碳小区”的概率；
（2）假定选择的“非低碳小区”为小区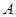
，调查显示其“低碳族”的比例为1:2，数据如图1所示，经过大力宣传，三个月后又进行一次调查，数据如图2所示，问这时小区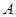是否达到“低碳小区”的标准？
（本小题满分14分）计算下列各式：
（1）
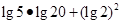
（2）
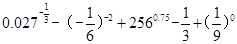
（本小题满分14分）若函数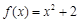
，
的定义域都是集合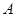
，函数
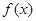和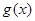
的值域分别为
和
.
（1）若
，求
；
（2）若
，且
，求实数m的值.
（本小题满分13分）已知函数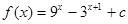
（其中
是常数）.
（1）若当
时,恒有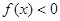
成立,求实数的取值范围；
（2）若存在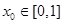
,使
成立,求实数的取值范围；
（3）若方程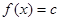
·
在
上有唯一实数解,求实数的取值范围.
（本小题满分13分）对于定义域为D的函数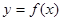
，若同时满足下列条件：①
在D内单调递增或单调递减；②存在区间[
]
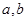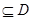，使在[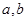]上的值域为[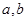]；那么把（
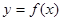）叫闭函数。
（1）求闭函数
符合条件②的区间[]；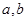
（2）判断函数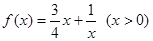
是否为闭函数？并说明理由；
（3）判断函数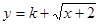
是否为闭函数？若是闭函数，求实数
的取值范围。
（本小题满分13分）如图，在三棱柱
中，四边形
是边长为4的正方形，平面
⊥平面，
．
（Ⅰ）求证：
⊥平面；
（Ⅱ）若点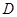
是线段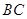
的中点，请问在线段
是否存在点
，使得
面？若存在，请说明点的位置，若不存在，请说明理由；
（Ⅲ）求二面角
的大小．