如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
(1)已知角 终边经过点P(-4,3),求
终边经过点P(-4,3),求 的值?
的值?
(2)已知函数 ,(b>0)在
,(b>0)在 的最大值为
的最大值为 ,最小值为-
,最小值为- ,求2a+b的值?
,求2a+b的值?
计算:
⑴ ;
;
(2)
(本小题满分15分)
若函数f(x)=ax3+bx2+cx+d是奇函数,且f(x)极小值=f(-)=-.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
(本小题满分14分)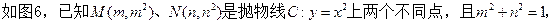
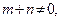 直线
直线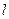 是线段
是线段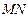 的垂直平分线.设椭圆E的方程为
的垂直平分线.设椭圆E的方程为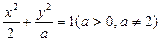 .
.
(1)当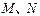 在
在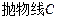 上移动时,求直线
上移动时,求直线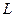 斜率
斜率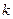 的取值范围;
的取值范围;
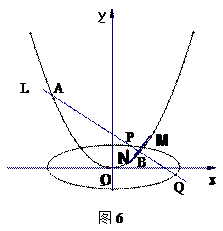
(2)已知直线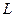 与抛物线
与抛物线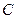 交于A、B两个不同点,
交于A、B两个不同点, 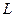 与椭圆
与椭圆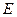 交于P、Q两个不同点,设AB中点为
交于P、Q两个不同点,设AB中点为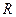 ,OP中点为
,OP中点为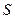 ,若
,若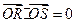 ,求椭圆
,求椭圆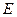 离心率的范围。
离心率的范围。
(本小题满分15分)
如图5,在底面为直角梯形的四棱锥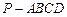
 中,
中,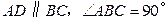 ,
, .
.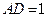 ,
,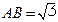 ,
,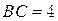 .
.
(1)求证: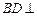
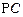 ;
;
(2)求直线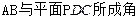 ;
;
(3)设点E在棱PC上,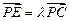 ,若
,若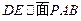 ,求
,求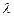 的值。
的值。