如图,动点M与两定点A(-1,0),B(2,0)构成△MAB,且∠MBA=2∠MAB.设动点M的轨迹为C.
(1)求轨迹C的方程;
(2)设直线 (其中
(其中 )与y轴相交于点P,与轨迹C相交于点Q,R,且
)与y轴相交于点P,与轨迹C相交于点Q,R,且 ,求
,求 的取值范围.
的取值范围.
已知函数 ,
,
(1)求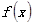 的单调区间和极值。 (2)求
的单调区间和极值。 (2)求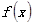 在
在 上的最大值和最小值。
上的最大值和最小值。
已知函数f(x)=alnx-x2+1.
(1)若曲线y=f(x)在x=1处的切线方程为4x-y+b=0,求实数a和b的值;
(2)若a<0,且对任意x1、x2∈(0,+∞),都|f(x1)-f(x2)|≥|x1-x2|,求a的取值范围.
三个求职者到某公司应聘,该公司为他们提供了A,B,C,D四个岗位,每人从中任选一个岗位。
(1)求恰有两个岗位没有被选的概率;
(2)设选择A岗位的人数为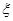 ,求
,求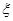 的分布列及数学期望。
的分布列及数学期望。
数列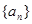 ,满足
,满足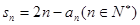
(1)求 ,并猜想通项公式
,并猜想通项公式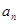 。
。
(2)用数学归纳法证明(1)中的猜想。
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程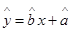 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?
(注: )
)