三个求职者到某公司应聘,该公司为他们提供了A,B,C,D四个岗位,每人从中任选一个岗位。
(1)求恰有两个岗位没有被选的概率;
(2)设选择A岗位的人数为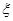 ,求
,求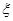 的分布列及数学期望。
的分布列及数学期望。
(本小题满分8分)已知集合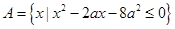 .
.
(Ⅰ)当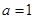 时,求集合
时,求集合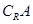 ;
;
(Ⅱ)若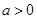 ,且
,且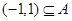 ,求实数
,求实数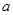 的取值范围.
的取值范围.
(本小题满分8分)计算:
(Ⅰ)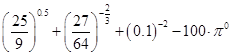 ;
;
(Ⅱ)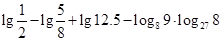 +
+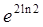 .
.
如图,椭圆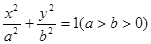 的一个 焦点是F(1,0),O为坐标原点.
的一个 焦点是F(1,0),O为坐标原点.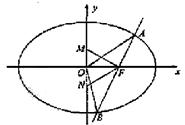
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;
(Ⅱ)设过点F的直线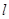 交椭圆于A、B两点,若直线
交椭圆于A、B两点,若直线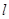 绕点F任意转动,恒有
绕点F任意转动,恒有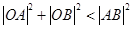 , 求
, 求 的取值范围.
的取值范围.
设过点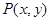 的直线分别与
的直线分别与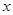 轴和
轴和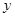 轴交于
轴交于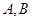 两点,点
两点,点 与点
与点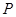 关于
关于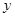 轴对称,
轴对称,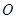 为坐标原点,若
为坐标原点,若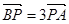 且
且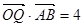 .
.
(Ⅰ)求点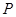 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过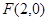 的直线与轨迹
的直线与轨迹 交于
交于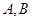 两点,求
两点,求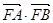 的取值范围.
的取值范围.
如图,已知四棱锥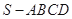 中,
中,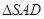 是边长为
是边长为 的正三角形,平面
的正三角形,平面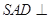 平面
平面 ,四边形
,四边形 是菱形,
是菱形, ,
,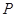 是
是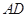 的中点,
的中点, 是
是 的中点.
的中点.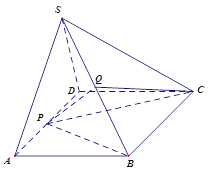
(Ⅰ)求证: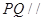 平面
平面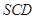 .
.
(Ⅱ)求二面角 的余弦值.
的余弦值.