(本小题满分12分) 如图,已知平面 ∩平面
∩平面 =AB,PQ⊥
=AB,PQ⊥ 于Q,PC⊥
于Q,PC⊥ 于C,CD⊥
于C,CD⊥ 于D.
于D.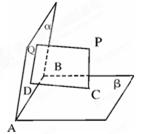
(1)求证:P、C、D、Q四点共面;
(2)求证:QD⊥AB.
如图,已知四棱台
上、下底面分别是边长为3和6的正方形,
,且
底面
,点
分别在棱
上.

(1)若
是
的中点,证明:
;
(2)若
平面
,二面角
的余弦值为
,求四面体
的体积.
某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为
,求
的分布列和数学期望.
设
的内角
的对边分别为
,且
为钝角.
(1)证明:
;
(2)求
的取值范围.
设
,且
.
(1)
;
(2)
与
不可能同时成立.
已知直线
(
为参数),以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线
的极坐标方程为
.
(1)将曲线
的极坐标方程化为直角坐标方程;
(2)设点
的直角坐标为
,直线
与曲线
的交点为
,求
的值.