已知数列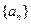 的前n项和为
的前n项和为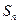 ,
, ,
,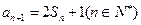 ,等差数列
,等差数列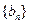 中
中
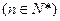 ,且
,且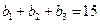 ,又
,又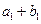 、
、 、
、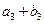 成等比数列.
成等比数列.
(Ⅰ)求数列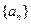 、
、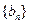 的通项公式;
的通项公式;
(Ⅱ)求数列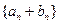 的前n项和Tn.
的前n项和Tn.
已知数列 和
和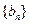 满足
满足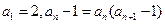 ,
, ,
, .
.
(1)求数列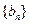 的通项公式;
的通项公式;
(2)设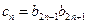 ,求使得
,求使得
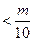 对一切
对一切 都成立的最小正整数
都成立的最小正整数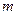 ;
;
(3)设数列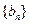 的前
的前 和为
和为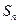 ,
,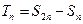 ,试比较
,试比较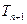 与
与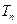 的大小.
的大小.
已知点C(1,0),点A、B是⊙O: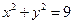 上任意两个不同的点,
上任意两个不同的点,
且满足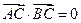 ,设P为弦AB的中点,
,设P为弦AB的中点,
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线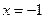 的
的
距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE
为平行四边形,DC 平面ABC ,
平面ABC , ,
, .
.
(1)证明:平面ACD 平面
平面 ;
;
(2)记 ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求 的表达式;
的表达式;
 (3)当
(3)当 取得最大值时,求证:AD=CE.
取得最大值时,求证:AD=CE.
“根据《中华人民共和国道路交通安全法》规定:
车辆驾驶员血液酒精浓度在20—80 mg/100ml(不含80)
之间,属于酒后驾车,血液酒精浓度在80mg/100ml (含80)以上时,属醉酒驾车.”
(含80)以上时,属醉酒驾车.”
2009年8月15日晚8时开始某市交警一队在该市
一交通岗前设点对过往的车辆进行抽查,经过两个小时
共查出酒后驾车者60名,图甲是用酒精测试仪对这60
名酒后驾车者血液中酒精浓度进行检测后依所得结果画
出的频率分布直方图.
(1)求这60名酒后驾车者中属醉酒驾车的人数;
(图甲中每组包括左端点,不包括右端点)
(2)统计方法中,同一组数据常用该组区间的中点
值作为代表,图乙的程序框图是对这60名酒后驾车者
血液的酒精浓度做进一步的统计,求出图乙输出的S值,
并说明S的统计意义;(图乙中数据 与
与 分别表示图图乙
分别表示图图乙
甲中各组的组中值及频率)
(3)本次行动中,吴、李两位先生都被酒精测试仪测得酒精浓度在70 (含70)以上,但他俩坚称没喝那么多,是测试仪不准,交警大队陈队长决定在被酒精测试仪测得酒精浓度在70
(含70)以上,但他俩坚称没喝那么多,是测试仪不准,交警大队陈队长决定在被酒精测试仪测得酒精浓度在70 (含70)以上的酒后驾车者中随机抽出2人抽血检验,求吴、李两位先生至少有1人被抽中的概率.
(含70)以上的酒后驾车者中随机抽出2人抽血检验,求吴、李两位先生至少有1人被抽中的概率.
在△ABC中,角A、B、C所对的边分别为a、b、c(其中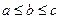 ),设向量
),设向量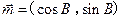 ,
,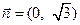 ,且向量
,且向量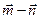 为单位向量.
为单位向量. (1)求∠B的大小;
(1)求∠B的大小;
(2)若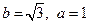 ,求△ABC的面积.
,求△ABC的面积.