在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=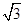 acosB.
acosB.
(1)求角B的大小;
(2)若a=2,△ABC的面积为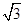 ,求b,c.
,求b,c.
(本小题满分10分)
已知平面向量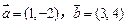 .
.
(1)求向量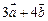 的坐标;
的坐标;
(2)当实数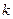 为何值时,
为何值时,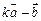 与
与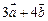 共线.
共线.
(本小题满分12分)
设函数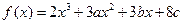 在
在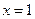 及
及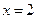 时取得极值;
时取得极值;
(Ⅰ)求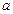 与b的值;
与b的值;
(Ⅱ)若对于任意的 ,都有
,都有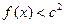 成立,求c的取值范围。
成立,求c的取值范围。
(本小题满分12分)
如图,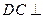 平面
平面 ,
, ,
, ,
,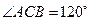 ,
, 分别为
分别为 的中点.
的中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求 与平面
与平面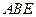 所成角的正弦值。
所成角的正弦值。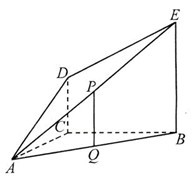
(本小题满分12分)
设a为实数,函数
(Ⅰ)求f(x)的极值;
(Ⅱ)当 在什么范围内取值时,曲线y= f(x)与x轴仅有一个交点。
在什么范围内取值时,曲线y= f(x)与x轴仅有一个交点。
(本小题满分12分)
三人独立破译同一份密码.已知三人各自破译出密码的概率分别为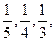 且他们是否破译出密码互不影响.
且他们是否破译出密码互不影响.
(Ⅰ)求恰有二人破译出密码的概率;
(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由.