已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若A⊆∁RB,求实数m的取值范围.
(本小题满分14分)已知三棱锥 中,
中, ,
, .如图,从由任何二个顶点确定的向量中任取两个向量,记变量
.如图,从由任何二个顶点确定的向量中任取两个向量,记变量 为所取两个向量的数量积的绝对值.
为所取两个向量的数量积的绝对值.
(1)当 时,求
时,求 的值.
的值.
(2)当 时,求变量
时,求变量 的分布列与期望.
的分布列与期望.
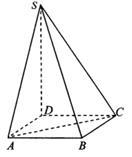
(本小题满分13分)如图,四棱锥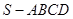 的底面是正方形,
的底面是正方形,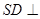 平面
平面 ,
,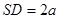 ,
,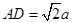 ,点
,点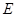 是
是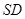 上的点,且
上的点,且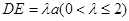 .
.
(1)求证:对任意的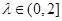 ,都有
,都有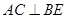 .
.
(2)设二面角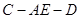 的大小为
的大小为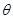
 ,直线
,直线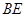 与平面
与平面 所成的角为
所成的角为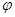 ,若
,若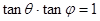 ,求
,求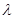 的值.
的值.
(本小题满分12分)某青年教师专项课题进行“学生数学成绩与物理成绩的关系”的课题研究,对于高二年级 800名学生上学期期末数学和物理成绩,按优秀和不优秀分类得结果:数学和物理都优秀的有60人,数学成绩优秀但物理不优秀的有140人,物理成绩优秀但数学不优秀的有100人.
(1)能否在犯错概率不超过0.001的前提下认为该校学生的数学成绩与物理成绩有关系?
(2)将上述调查所得到的频率视为概率,从全体高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记抽取的3个成绩中数学、物理两科成绩至少有一科优秀的次数为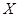 ,求
,求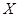 的期望
的期望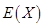 .
.
附: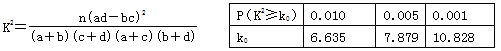
(本小题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,补全这个频率分布直方图;并估计该校学生的数学成绩的中位数.
(2)从数学成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
(3)若从全市参加高一年级期末考试的学生中,任意抽取4个学生,设这四个学生中数学成绩为80分以上(包括80分)的人数为X,(以该校学生的成绩的频率估计概率),求X的数学期望.