已知 且
且 ,函数
,函数 ,
,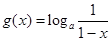 ,记
,记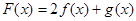
(Ⅰ)求函数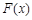 的定义域
的定义域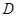 及其零点;
及其零点;
(Ⅱ)若关于 的方程
的方程 在区间
在区间 内仅有一解,求实数
内仅有一解,求实数 的取值范围.
的取值范围.
(本小题满分13分)已知数列 满足
满足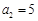 ,且其前
,且其前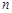 项和
项和 .
.
(Ⅰ)求 的值和数列
的值和数列 的通项公式;
的通项公式;
(Ⅱ)设数列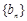 为等比数列,公比为
为等比数列,公比为 ,且其前
,且其前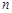 项和
项和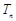 满足
满足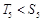 ,求
,求 的取值范围.
的取值范围.
(本小题满分13分)已知函数 ,x∈R .
,x∈R .
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)判断函数 在区间
在区间 上是否为增函数?并说明理由.
上是否为增函数?并说明理由.
(本小题满分13分)设函数 ,对于任意给定的
,对于任意给定的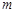 位自然数
位自然数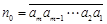 (其中
(其中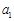 是个位数字,
是个位数字, 是十位数字,
是十位数字, ),定义变换
),定义变换 :
: . 并规定
. 并规定 .记
.记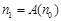 ,
, ,
, ,
,  ,
, .
.
(Ⅰ)若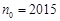 ,求
,求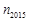 ;
;
(Ⅱ)当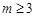 时,证明:对于任意的
时,证明:对于任意的 位自然数
位自然数 均有
均有 ;
;
(Ⅲ)如果 ,写出
,写出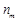 的所有可能取值.(只需写出结论)
的所有可能取值.(只需写出结论)
(本小题满分14分)已知椭圆C: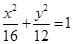 的右焦点为F,右顶点为A,离心率为e,点
的右焦点为F,右顶点为A,离心率为e,点 满足条件
满足条件 .
.
(Ⅰ)求m的值;
(Ⅱ)设过点F的直线l与椭圆C相交于M,N两点,记 和
和 的面积分别为
的面积分别为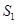 ,
, ,求证:
,求证: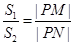 .
.
(本小题满分13分)已知函数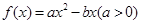 和
和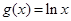 的图象有公共点P,且在点P处的切线相同.
的图象有公共点P,且在点P处的切线相同.
(Ⅰ)若点P的坐标为 ,求
,求 的值;
的值;
(Ⅱ)已知 ,求切点P的坐标.
,求切点P的坐标.