已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切. 是椭圆
是椭圆 的右顶点与上顶点,直线
的右顶点与上顶点,直线 与椭圆相交于
与椭圆相交于 两点.
两点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当四边形 面积取最大值时,求
面积取最大值时,求 的值.
的值.
(本小题满分12分)在数列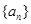 中,
中,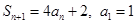 ;
;
(1)设 ,求证数列
,求证数列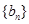 是等比数列;
是等比数列;
(2)设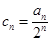 ,求证:数列
,求证:数列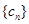 是等差数列;
是等差数列;
(3)求数列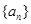 的通项公式及前n项和的公式。
的通项公式及前n项和的公式。
(本小题满分12分)已知 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线,
轴上的双曲线, :方程
:方程 =(
=( 一
一 )
) 表示开口向右的抛物线.若“
表示开口向右的抛物线.若“

 ”为真命题,“
”为真命题,“

 ”为假命题,求实数
”为假命题,求实数 的范围.
的范围.
(本小题满分12分)点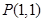 为椭圆
为椭圆 内的一定点,过P点引一直线,与椭圆相交于
内的一定点,过P点引一直线,与椭圆相交于 两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。
两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。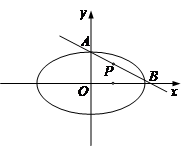
(本小题满分12分)已知双曲线的一条渐近线方程是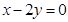 ,若双曲线经过点
,若双曲线经过点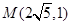 ,求此双曲线的标准方程。
,求此双曲线的标准方程。
(本小题两小题,每题6分,满分12分)
⑴对任意 ,试比较
,试比较 与
与 的大小;
的大小;
⑵已知函数 的定义域为R,求实数k的取值范围。
的定义域为R,求实数k的取值范围。