已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线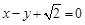 相切.
相切. 是椭圆
是椭圆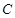 的右顶点与上顶点,直线
的右顶点与上顶点,直线 与椭圆相交于
与椭圆相交于 两点.
两点.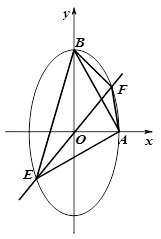
(Ⅰ)求椭圆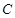 的方程;
的方程;
(Ⅱ)当四边形 面积取最大值时,求
面积取最大值时,求 的值.
的值.
双曲线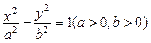 的左、右焦点分别为
的左、右焦点分别为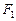 、
、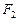 ,
, 为坐标原点,点
为坐标原点,点 在双曲线的右支上,点
在双曲线的右支上,点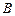 在双曲线左准线上,
在双曲线左准线上,
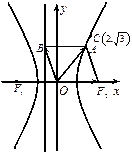
(Ⅰ)求双曲线的离心率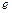 ;
;
(Ⅱ)若此双曲线过 ,求双曲线的方程;
,求双曲线的方程;
(Ⅲ)在(Ⅱ)的条件下, 、
、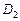 分别是双曲线的虚轴端点(
分别是双曲线的虚轴端点(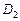 在
在 轴正半轴上),过
轴正半轴上),过 的直线
的直线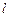 交双曲线
交双曲线 、
、 ,
,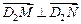 ,求直线
,求直线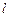 的方程
的方程
设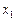 ,
, 是函数
是函数 的两个极值点,且
的两个极值点,且
 ..
..
(Ⅰ)用 表示
表示 ,并求
,并求 的最大值;
的最大值;
(Ⅱ)若函数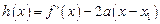 ,求证:当
,求证:当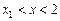 且
且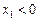 时,
时,
对于数列 ,定义
,定义 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 .
.
(Ⅰ)若数列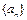 的通项公式
的通项公式 ,求
,求 的通项公式;
的通项公式;
(Ⅱ)若数列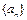 的首项是1,且
的首项是1,且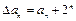 .
.
①设
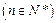 ,求数列
,求数列 的通项公式;
的通项公式;
②求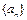 的前
的前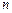 项和
项和 .
.
甲、乙、丙三人分别独立解一道题,甲做对的概率是 ,甲、乙、丙三人都做对的概率是
,甲、乙、丙三人都做对的概率是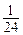 ,甲、乙、丙全部做错的概率是
,甲、乙、丙全部做错的概率是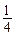 .
.
(Ⅰ)分别求乙、丙两人各自做对这道题的概率;
(Ⅱ)求甲、乙、丙中恰有一个人做对这道题的概率
在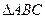 中,
中, 所对边分别为
所对边分别为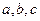 .已知
.已知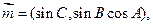
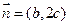 ,且
,且 .
.
(Ⅰ)求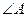 大小.
大小.
(Ⅱ)若 求
求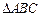 的面积
的面积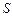 的大小.
的大小.