甲、乙、丙三班进行知识竞赛,每两班比赛一场,共赛三场.每场比赛胜者得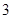 分,负者得
分,负者得 分,没有平局,在每一场比赛中,甲班胜乙班的概率为
分,没有平局,在每一场比赛中,甲班胜乙班的概率为 ,甲班胜丙班的概率为
,甲班胜丙班的概率为 ,乙班胜丙班的概率为
,乙班胜丙班的概率为 .
.
(Ⅰ)求甲班获第一名且丙班获第二名的概率;
(Ⅱ)设在该次比赛中,甲班得分为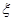 ,求
,求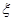 的分布列和数学期望.
的分布列和数学期望.
如图,某中学甲、乙两班共有25名学生报名参加了一项测试.这25位学生的考分编成的茎叶图,其中有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.
(1)求这两个班学生成绩的中位数及x的值;
(2)如果将这些成绩分为“优秀”(得分在175分以上,包括175分)和“过关”,若学校再从这两个班获得“优秀”成绩的考生中选出3名代表学校参加比赛,求这3人中甲班至多有一人入选的概率.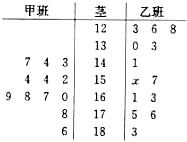
已知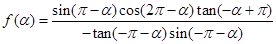
(1)化简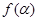 ;
;
(2)若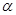 是第三象限角,且cos(
是第三象限角,且cos( )=
)= ,求
,求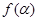 的值.
的值.
已知函数 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式 存在实数解,求实数
存在实数解,求实数 的取值范围.
的取值范围.
在平面直角坐标系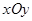 中,曲线
中,曲线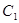 的参数方程为
的参数方程为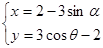 ,(其中
,(其中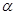 为参数,
为参数,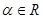 ),在极坐标系(以坐标原点
),在极坐标系(以坐标原点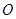 为极点,以
为极点,以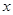 轴非负半轴为极轴)中,曲线
轴非负半轴为极轴)中,曲线 的极坐标方程为
的极坐标方程为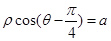 .
.
(1)把曲线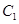 和
和 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线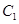 上恰有三个点到曲线
上恰有三个点到曲线 的距离为
的距离为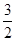 ,求曲线
,求曲线 的直角坐标方程.
的直角坐标方程.
如图,半圆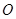 的直径
的直径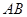 的长为4,点
的长为4,点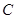 平分弧
平分弧 ,过
,过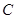 作
作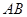 的垂线交
的垂线交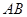 于
于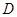 ,交
,交 于
于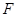 .
.
(1)求证: :
:
(2)若 是
是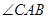 的角平分线,求
的角平分线,求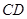 的长.
的长.