已知椭圆 的离心率为
的离心率为 ,右焦点为(
,右焦点为( ,0),过点
,0),过点 斜率为1的直线
斜率为1的直线 与椭圆
与椭圆 交于
交于 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)求弦 的长.
的长.
已知函数 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
.
(1)求 的值;
的值;
(2)在 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,求
,求 的取值范围.
的取值范围.
已知双曲线 =1的离心率为2,焦点到渐近线的距离等于
=1的离心率为2,焦点到渐近线的距离等于 ,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
(1)求双曲线的方程;
(2)若△F1AB的面积等于6 ,求直线l的方程.
,求直线l的方程.
根据下列条件,求双曲线方程.
(1)与双曲线 =1有共同的渐近线,且过点(-3,2
=1有共同的渐近线,且过点(-3,2 );
);
(2)与双曲线 =1有公共焦点,且过点(3
=1有公共焦点,且过点(3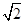 ,2).
,2).
双曲线C与椭圆 =1有相同的焦点,直线y=
=1有相同的焦点,直线y= x为C的一条渐近线.求双曲线C的方程.
x为C的一条渐近线.求双曲线C的方程.
已知双曲线过点(3,-2),且与椭圆4x2+9y2=36有相同的焦点.
(1)求双曲线的标准方程;
(2)求以双曲线的右准线为准线的抛物线的标准方程.