已知函数
，
（
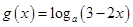，且
）．
（1）求函数
的定义域；
（2）判断函数的奇偶性，并予以证明．
在周长为定值的
中，已知
，且当顶点
位于定点
时，
有最小值为
.(1)建立适当的坐标系，求顶点的轨迹方程.(2)过点
作直线与(1)中的曲线交于
、
两点，求
的最小值的集合.
在平面直角坐标系xoy中，给定三点
，点P到直线BC的距离是该点到直线AB，AC距离的等比中项。（Ⅰ）求点P的轨迹方程；（Ⅱ）若直线L经过
的内心（设为D），且与P点的轨迹恰好有3个公共点，求L的斜率k的取值范围。
已知点A
和曲线
上的点
…、
。若
、
、…、
成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若
,是否存在满足条件的
.若存在,求出n可取的所有值,若不存在,说明理由.
已知曲线
，
，
为正常数．直线
与曲线
的实轴不垂直，且依次交直线
、曲线、直线
于
、
、
、
4个点，
为坐标原点．
（1）若
，求证：
的面积为定值；
（2）若
的面积等于面积的
，求证：．
设
、
、
满足
，若对于任意
求